UMSM

11-12 Sep 2014 Paris (France)

Program > Plenary and keynote lectures

Keynotes

A special feature of the colloquium will be the Plenary Lectures. Each day will start off with a plenary lecture by an eminent scientist on a topic of interest to all.

Smart structures and active control of vibrations: 25 years of research at ULB

André J. Preumont 1,2

André Preumont received his MSc in Aeronautics from the university of Liege in 1973 and his PhD in Applied Sciences in 1981. He spent 10 years in industry before moving in academia. He has been a professor of Mechanical Engineering and Robotics at the Université Libre de Bruxelles (ULB) since 1987, full professor since 1991, and director of the Active Structures Laboratory. He is the author of 7 books. He is a member of the Belgian Royal Academy and was the recipient of the Alexander von Humboldt Research Award in 2011. He was a visiting professor at Virginia Tech (USA), UT Compiègne and INSA Lyon (France). He is a Fellow of the American Institute of Aeronautics and Astronautics.

1 : Université Libre de Bruxelles [Bruxelles] (ULB) - Website

Avenue Franklin Roosevelt 50 - 1050 Bruxelles - Belgium

2 : ULB Department of Mechanical Engineering and Robotics CP 165/42 Active Structures Laboratory (ULB) - Website

Active Structures Laboratory avenue F.D.Roosevelt, 50 B-1050 Brussels Belgium - Belgium

Over the past 25 years, the Active Structures Laboratory of ULB has been pioneering active techniques for vibration control in various applications, mostly related to future space projects, precision engineering and bridges. The emphasis is placed on robustness and on the ability to develop a controller with a limited knowledge of the structure. The talk is divided into several parts:

The first part is devoted to the passive damping with piezoelectric transducers: This technology consists of transforming the vibrational energy into electrical energy which is dissipated in a passive network; it often involves active components (synthetic inductors, negative capacitors) and may be extended to applications requiring a negative damping.

The second part focuses of the vibration isolation and damping in large space structures: These applications highlight the importance of collocated control and illustrate how a clever passive design may sometimes compete successfully with an active one. An active member consisting of a linear piezoelectric actuator collocated with a force sensor is described (it works like as muscle). The Integral Force Feedback (IFF) controller exhibits very good robustness properties.

Next, the talk applies the IFF controller to the active tendon control of string and cable structures and discusses how the nonlinearities of the cable dynamics may be handled, in order to reduce the numerical effort in building complex models (this part may have some aspects of interest for modeling string instruments). Active vibration control is illustrated with the control of parametric vibration of a cable-stayed bridge.

Finally, the talk includes two additional parts (if time allows) which can be seen as nice examples of mechatronics: one on real-time sound radiation sensor (discrete sensor array and distributed sensor) and one on deformable mirrors actuated with an array of piezoelectric actuators used for adaptive optics.

References:
A.Preumont, Vibration Control of Active Structures, An Introduction, 3rd ed. (Springer) in 2011.
A.Preumont, Mechatronics: Dynamics of Electromechanical and Piezoelectric Systems, Springer 2006.
A.Preumont, K. Seto, Active Control of Structures, Wiley, 2008.

Subject :	:	Plenary lecture
Topics	:	Active control of vibration

Multisymplectic geometry: some perspectives

Frédéric Hélein 1,2

Frédéric Hélein is professor at the Université Paris Diderot in mathematics. He has worked on the analysis of elliptic partial differential equations in geometry, geometric completely integrable systems and he is now oriented towards questions in mathematical physics, using e.g. multisymplectic geometry to understand the classical and quantum fields theories.
He received his PhD in Mathematics at the Ecole Polytechnique in 1989 under the supervision of Jean-Michel Coron and his Habilitation at the University of Paris Orsay in 1991. He has been professor at the Ecole Normale Supérieure de Cachan since 1991 and 2003. He won the Fermat prize in 1999.

1 : Université Paris 7, Paris Diderot (UP7) - Website

Université Paris VII - Paris Diderot

5 rue Thomas-Mann - 75205 Paris cedex 13 - France

2 : Institut de Mathématiques de Jussieu (IMJ) - Website

CNRS : UMR7586

2, place Jussieu 75251 Paris Cedex 05 - France

Since Fermat's principle in optics and Least Action principle in mechanics, the calculus of variation has been applied to almost all fundamental laws of mathematical physics with a great success. The resulting equations, known as the Euler-Lagrange equations, can be translated in the form of the Hamilton equations, the meaning of which is independent on the choice of coordinates and can be expounded geometrically. This means that one may sometime avoid messy computations. For variational problems with one variable (i.e. the time variable) this leads to the so-called symplectic geometry. For instance Noether's (first) theorem, which is one of the most important result of this theory, connecting symmetries and conserved quantities, has a particularly concise translation in symplectic geometry.
However the validity of the calculus of variation and of Noether's theorem is not limited to the calculus of variations with one variable and can be applied to problems with several variables, for instance the four coordinates of our space-time. An analogue of the symplectic geometry, called multisymplectic geometry, can be built. It leads to similar results but also to deep differences. We will present this setting and its motivations, in particular for understanding classical and quantum physics.

Subject :	:	Plenary lecture
Topics	:	Symplectic and Poisson geometry and their applications to mechanics

Introductory sessions

Geometric aspects of active constraints

Jean-Pierre Marco 1,2

Jean-Pierre Marco focuses on dynamical systems and symplectic geometry, more specifically on geometric perturbation theory and dynamical complexity of intégrable and nearly integrable Hamiltonian systems (Arnold diffusion).

1 : Université Pierre et Marie Curie - Paris 6 (UPMC) - Website

Université Pierre et Marie Curie (UPMC) - Paris VI, IMJ

4, place Jussieu - 75005 Paris - France

2 : Institut de Mathématiques de Jussieu (IMJ) - Website

IMJ

Tour 15, 4 place Jussieu 75252 Paris cedex 05 – France

We will give an overview of various geometric formalisms used to describe the dynamics of a mechanical system submitted to an external control by moving holonomic constraints.

Subject :	:	Introductory session
Topics	:	Geometry of mechanical systems with active constraints

Modal active control of linear structures. Applications to musical instruments

Adrien Mamou-Mani 1

Adrien Mamou-Mani is a researcher in acoustics and mechanics applied to musical instruments at Ircam, and a professor in musical acoustics at Conservatoire de Paris (CNSMDP). Prior to these positions, he was successively Research Fellow at Cité de la Musique (Paris) and Newton International Fellow at the Open University (UK). Adrien earned an MSc in Sciences applied to Music at Université Pierre et Marie Curie (UPMC, Paris) and Ircam, and a PhD in Mechanics and Acoustics at UPMC. His main interests are the applications of science and technology for musical instrument making, including modelling and active control of vibration.

Baptiste Chomette 2

Baptiste Chomette is graduated engineer from ENSAM (Paris, France) in 2005 and received his PhD in Mechanical in 2008 from INSA Lyon (France). He is assistant professor in Institut Jean Le Rond d'Alembert since 2009. Its field of research are about smart materials and structures, vibration control and system identification, modelling and cracks detection, and finally musical acoustics in collaboration with IRCAM since 2010.

1 : UMR STMS (Ircam/CNRS/UPMC) Website

IRCAM

1 place Stravinsky, 75004 Paris - France

2 : Institut Jean Le Rond d'Alembert (IJLRA) - Website

Université Pierre et Marie Curie (UPMC) - Paris VI

Boite 162 4 place Jussieu 75005 Paris - France

Modal active control has been successfully applied to the vibration reduction of mechanical systems. This method initialy developped to target the control only on the mode of interest and to minimize the number of actuators and sensors also has the potential for adjusting finely the modal frequencies and dampings of musical instruments. After introducing the modal active control approach, applications on the cello, the guitar, and on a simplified clarinet will be presented, focusing on the effects on the sound and playability of these instruments.

Subject :	:	Introductory session
Topics	:	Active control of vibration
Topics	:	Sound synthesis & musical instruments

Wave turbulence in thin vibrating plates.
Application to the sound of cymbals and gongs

Cyril Touzé 1

Cyril Touzé works on geometrically nonlinear vibrations of thin shell structures. One aspects of his research is devoted to sound synthesis of cymbales ang gong-like instruments. These percussion instruments are known to vibrate in a strongly nonlinear regime, and thus exhibit a broadband Fourier spectrum, with an increase of energy to the high frequency range. This dynamics can be related to the wave turbulence motion displayed by thin plates that are also studied on the theoretical point of view.

1 : École Nationale Supérieure de Techniques Avancées (ENSTA ParisTech) - Website

ENSTA ParisTech

828, Boulevard des Maréchaux 91762 Palaiseau CEDEX - France

...

Subject :	:	Introductory session
Topics	:	Non-linear vibration

Coordinate free formulation of the vibrations of a Reissner beam and some mechanical consequences

J. Lerbet 1

Jean Lerbet 1

Jean Lerbet is Professor at Evry-Val-d’Essonne University. His work focuses on calculations on Lie groups and singularities of maps related to the kinematics and the dynamics of discrete and/or continuous systems. Its research also involves stability of non-conservative systems and the study of its kinematical structural stability.

1 : Université d'Evry Val d'Essonne (UEVE)- Website

Université d'Evry-Val d'Essonne

40 rue du Pelvoux CE1455 Courcouronnes 91020 Evry - France

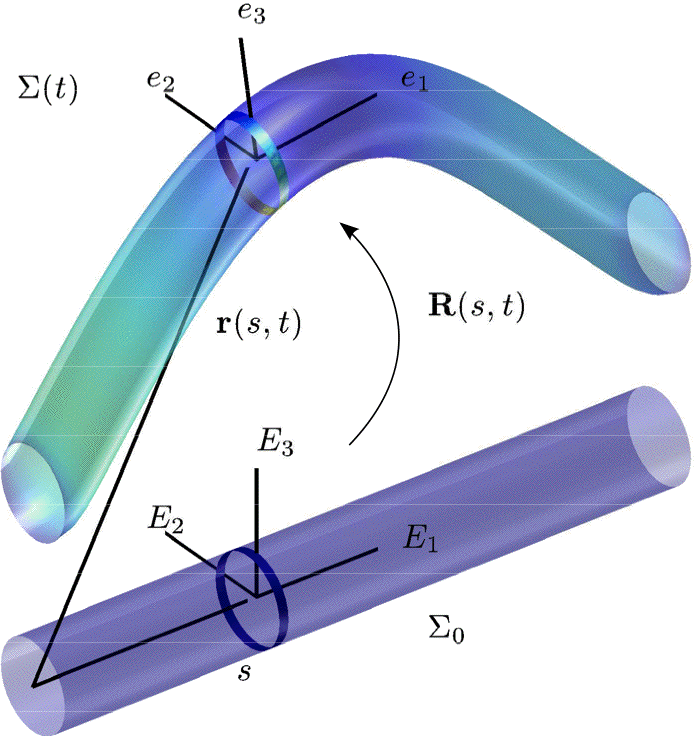
We start from a coordinate free model of a Reissner beam with 6 d.o.f. at each section. The dynamic model is brought back to a partial differential equation in the Lie algebra of the Lie group of Euclidean displacements. A coordinate free linearization with respect to any equilibrium position is done and some interesting results about proper modes are highlighted in the framework of linear elasticity. These calculations are performed without ever using any frame nor coordinate

Subject :	:	Abstract
Topics	:	Geometric methods in dynamical systems

Multisymplectic geometry with symmetry. Application to the Reissner beam

Joël Bensoam 1

Joël Bensoam initial research involved the investigation of numerical sound synthesis using Finite and Boundary Element Methods. More recently, he has been applying Geometric Mechanics to acoustics. Thanks to the use of differential geometry and Lie group theory, the non linear effects due to large displacements in an acoustical system can be handled.

1 : Institut de Recherche et Coordination Acoustique/Musique (IRCAM) - Website

IRCAM

1, place Igor Stravinsky 75004 Paris - France

Although acoustics is one of the disciplines of mechanics, its ”geometrization” is still limited to a few areas. The Reissner beam is one of the simplest acoustical system that can be treated in the context of mechanics with symmetry. It seems that the non-linear phenomena can be handled in their intrinsic qualities through the concepts of differential geometry. Using the symmetry of Lie groups, the geometric constructions needed for reduction are presented in the context of the ”covariant” approach.

Subject :	:	Introductory session
Topics	:	Symplectic and Poisson geometry and their applications to mechanics

Online user: 1

RSS Feed